परिवर्ती अनुपात का नियम आर्थिक सिद्धांत में एक महत्वपूर्ण स्थान रखता है। यह नियम उत्पादन फलन का अध्ययन करता है जब एक कारक परिवर्तनीय होता है और अन्य कारकों की मात्राएँ स्थिर रखी जाती हैं। अन्य शब्दों में, यह उस इनपुट-आउटपुट संबंध को दर्शाता है जब उत्पादन को एक इनपुट की मात्रा में परिवर्तन करके बढ़ाया जाता है। जब एक कारक की मात्रा को परिवर्तित किया जाता है और अन्य कारकों की मात्रा को स्थिर रखा जाता है, तो परिवर्तनीय कारक और स्थिर कारक के बीच का अनुपात बदल जाता है; जैसे-जैसे परिवर्तनीय कारक की मात्रा बढ़ाई जाती है, परिवर्तनीय कारक और स्थिर कारक का अनुपात निरंतर बढ़ता जाता है। चूँकि इस नियम के अंतर्गत हम उत्पादन पर कारक अनुपातों में परिवर्तन के प्रभाव का अध्ययन करते हैं, इसलिए इसे परिवर्ती अनुपात का नियम कहा जाता है। इस प्रकार, परिवर्ती अनुपात का नियम, शास्त्रीय अर्थशास्त्र के प्रसिद्ध “घटते प्रतिफल के नियम” का नया नाम है। इस नियम ने आर्थिक विचारधारा के इतिहास में एक महत्वपूर्ण भूमिका निभाई है और आधुनिक आर्थिक सिद्धांत में भी समान रूप से महत्वपूर्ण स्थान रखता है। इस नियम का समर्थन वास्तविक विश्व से प्राप्त प्रायोगिक साक्ष्यों द्वारा किया गया है। परिवर्ती अनुपात अथवा घटते प्रतिफल के नियम को विभिन्न अर्थशास्त्रियों ने निम्नलिखित प्रकार से प्रस्तुत किया है:
“जब कारकों के संयोजन में किसी एक कारक का अनुपात बढ़ाया जाता है, तो एक निश्चित बिंदु के बाद पहले उस कारक का सीमांत उत्पाद और फिर औसत उत्पाद घटने लगता है।” (एफ. बेनहम)
“कुछ इनपुट्स में वृद्धि, अन्य स्थिर इनपुट्स की तुलना में, प्रौद्योगिकी की एक निश्चित अवस्था में उत्पादन को बढ़ाएगी; लेकिन एक बिंदु के बाद अतिरिक्त इनपुट्स की समान वृद्धि से प्राप्त अतिरिक्त उत्पादन कम हो जाएगा।” (पॉल ए. सैमुएलसन)
मार्शल ने घटते प्रतिफल के नियम को कृषि के संदर्भ में चर्चा की। उन्होंने इस नियम को इस प्रकार परिभाषित किया है: “भूमि की खेती में लगाए गए पूँजी और श्रम की वृद्धि सामान्यतः उत्पाद की मात्रा में अनुपात से कम वृद्धि करती है, जब तक कि यह कृषि तकनीकों में सुधार के साथ मेल न खा जाए।”
उपरोक्त परिभाषाओं से यह स्पष्ट है कि परिवर्ती अनुपात का नियम उत्पादन के उस व्यवहार को दर्शाता है, जब एक कारक की मात्रा बढ़ाई जाती है और अन्य कारकों की मात्रा स्थिर रखी जाती है, तथा यह आगे बताता है कि सीमांत उत्पाद और औसत उत्पाद अंततः घटने लगेंगे।
परिवर्ती अनुपात के नियम की मान्यताएँ
परिवर्ती अनुपात का नियम निम्नलिखित मान्यताओं के अंतर्गत सही सिद्ध होता है:
1. प्रौद्योगिकी की अवस्था को स्थिर माना जाता है। अतः जब हम इस नियम का उपयोग करके उत्पादन फलन का विश्लेषण कर रहे होते हैं, तब प्रौद्योगिकी में कोई सुधार नहीं हो सकता। क्योंकि यदि प्रौद्योगिकी में सुधार की अनुमति दी जाए, तो समान स्तर के इनपुट्स के साथ बेहतर प्रौद्योगिकी उपलब्ध होने के कारण सीमांत और औसत उत्पाद बढ़ सकते हैं।
2. एक समय में केवल एक कारक को परिवर्तनीय माना जाता है और अन्य सभी कारकों को स्थिर माना जाता है, क्योंकि तभी हम यह अध्ययन कर सकते हैं कि परिवर्तनीय कारक में परिवर्तन के कारण उत्पादन में क्या परिवर्तन होगा।
3. परिवर्तनीय कारकों की विभिन्न इकाइयों को समरूप (Homogeneous) माना जाता है। क्योंकि यदि वे समरूप न हों, तो हम केवल परिवर्तनीय कारक में परिवर्तन का प्रभाव नहीं देख पाएँगे, बल्कि उत्पादन फलन परिवर्तनीय इनपुट की मात्रा में परिवर्तन के साथ-साथ इनपुट की गुणवत्ता में परिवर्तन का संयुक्त प्रभाव दिखाएगा। (विषम इनपुट्स का अर्थ है भिन्न गुणवत्ता)।
4. यह नियम इस संभावना पर आधारित है कि विभिन्न कारकों को किस अनुपात में संयोजित कर किसी उत्पाद का उत्पादन किया जा सकता है। यह नियम उन परिस्थितियों में लागू नहीं होता जहाँ कारकों का उपयोग उत्पाद प्राप्त करने के लिए स्थिर अनुपातों में ही करना आवश्यक हो। जोन रॉबिन्सन द्वारा प्रतिपादित यह नियम अल्पावधि विश्लेषण में व्यापक रूप से प्रयुक्त उत्पादन नियम है। यह नियम बताता है कि जब कोई उत्पादक स्थिर कारकों की दी गई मात्रा के साथ परिवर्तनीय कारक की लगातार इकाइयों को नियोजित करता है, तो प्रारंभ में सीमांत उत्पादकता बढ़ेगी, फिर घटेगी और अंततः नकारात्मक हो जाएगी।
अन्य शब्दों में, जब कोई उत्पादक स्थिर कारकों की दी गई मात्रा के साथ परिवर्तनीय कारक की अतिरिक्त इकाइयों को संयोजित करता है, तो कुल उत्पादन बढ़ता है, लेकिन एक निश्चित बिंदु के बाद घटने लगता है। हम इस नियम को एक सारणी और आरेख की सहायता से समझाएँगे। यहाँ यह माना गया है कि उत्पादन के लिए भूमि की मात्रा स्थिर है और श्रम ही एकमात्र परिवर्तनीय कारक है।
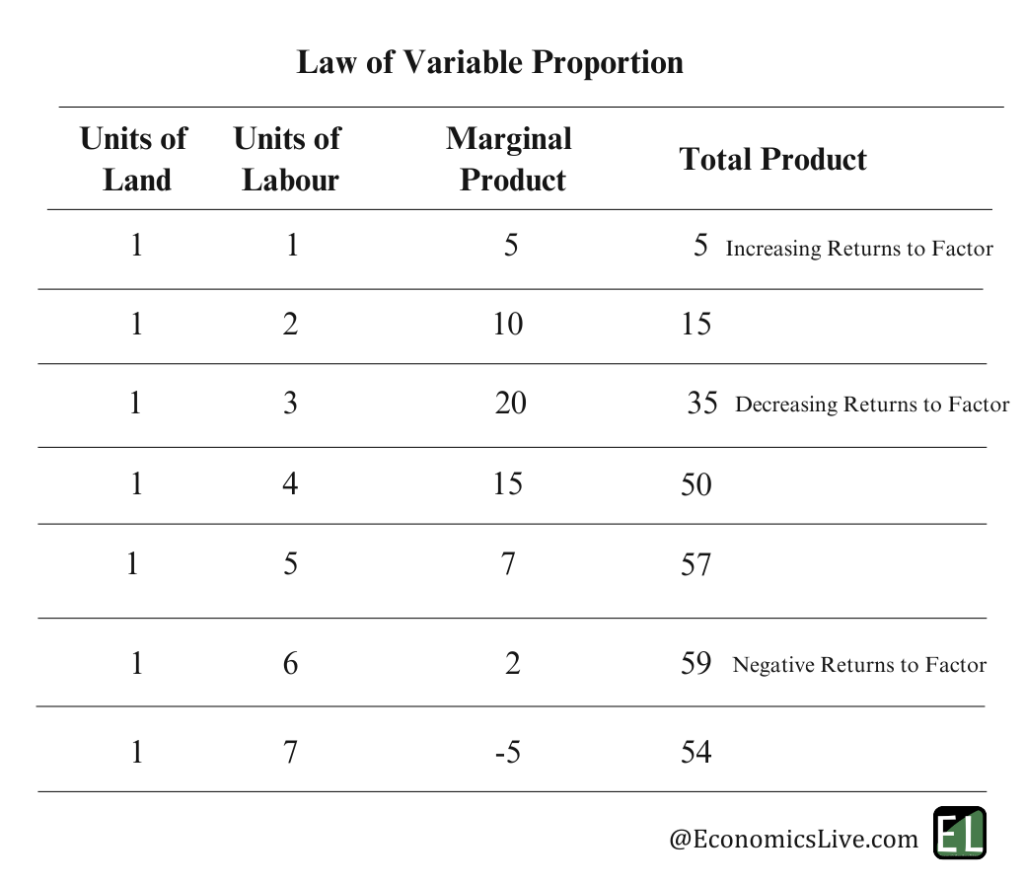
अतः, हम देखते हैं कि जैसे ही उत्पादक ने श्रम इनपुट को बढ़ाना जारी रखा, प्रारंभ में तीसरे श्रम इनपुट तक सीमांत उत्पाद बढ़ा, फिर तीसरी इकाई के बाद यह घटने लगा और छठी श्रम इकाई के बाद नकारात्मक हो गया, जिससे कारक पर नकारात्मक प्रतिफल उत्पन्न हुआ।
जब सीमांत उत्पाद (MP) बढ़ता है, तब कुल उत्पाद (TP) बढ़ती दर से बढ़ता है और जैसे ही MP घटने लगता है, TP तो बढ़ता है, लेकिन घटती दर से; और जब MP नकारात्मक हो जाता है, तब TP घटने लगता है।
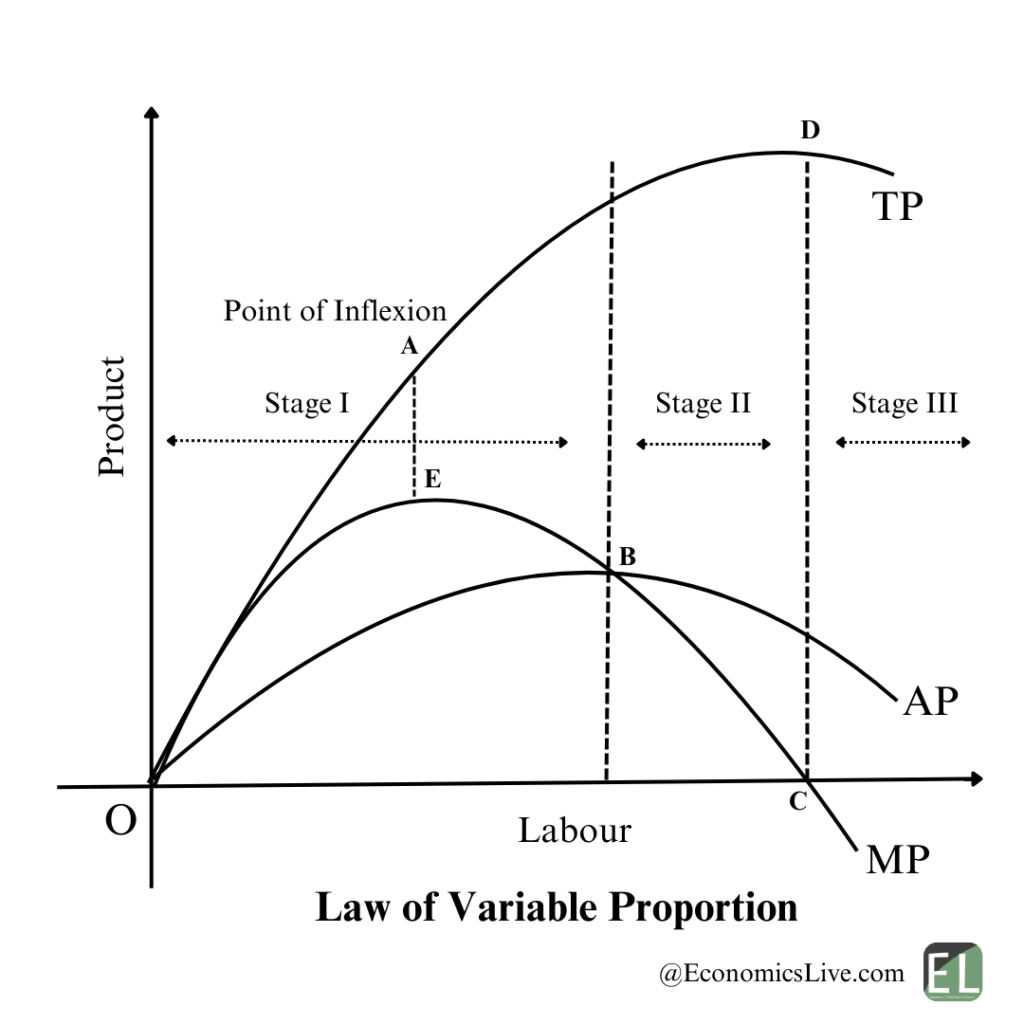
उपरोक्त आरेख में जैसा कि हम देख सकते हैं, जैसे ही श्रम इनपुट x-अक्ष पर बढ़ता है, श्रम का सीमांत उत्पाद (MP) बिंदु E तक बढ़ता है और उसके अनुरूप कुल उत्पाद (TP) बिंदु A तक बढ़ती दर से बढ़ता है। बिंदु A के बाद TP घटती दर से बढ़ता है। अतः बिंदु A को संक्रमण बिंदु (Point of Inflexion) भी कहा जाता है, क्योंकि TP वक्र की वक्रता बिंदु A पर बदल जाती है।
बिंदु B पर औसत उत्पाद (AP) अधिकतम होता है, जिसका अर्थ है कि बिंदु B पर AP = MP होता है। यह बिंदु उत्पादन के प्रथम चरण का अंत दर्शाता है, जिसे बढ़ते प्रतिफल का चरण भी कहा जाता है।
द्वितीय चरण में सीमांत उत्पाद (MP) लगातार घटता है और कुल उत्पाद (TP) घटती दर से बढ़ता है तथा अंततः बिंदु C पर x-अक्ष को छूता है, जहाँ MP = 0 होता है और इसके अनुरूप TP अपने अधिकतम बिंदु D पर होता है। बिंदु C के बाद तृतीय चरण प्रारंभ होता है, जिसे नकारात्मक प्रतिफल का चरण कहा जाता है।
एक तर्कसंगत उत्पादक हमेशा उत्पादन के द्वितीय चरण में कार्य करेगा। तृतीय चरण को अस्वीकार कर दिया जाता है क्योंकि इसमें नकारात्मक प्रतिफल मिलता है और प्रथम चरण में MP बढ़ रहा होता है और बाद में घटने लगता है, जिसका अर्थ है कि TP में अभी भी वृद्धि हो रही है। प्रथम चरण में उत्पादक नहीं रुकेगा क्योंकि उत्पादन के स्थिर कारकों का पूर्ण रूप से उपयोग उनकी संभावित क्षमता तक नहीं हुआ है।
अतः, एक तर्कसंगत उद्यमी प्रथम चरण में नहीं रुकेगा और अपना उत्पादन तब तक बढ़ाएगा जब तक सीमांत उत्पाद शून्य न हो जाए, अर्थात् जब तक MP = 0 न हो जाए। इसका अर्थ है कि अतिरिक्त परिवर्तनीय इनपुट को नियोजित करने से तब तक कुल उत्पाद (TP) में कुछ न कुछ योगदान होता रहेगा।
अतः यह स्पष्ट है कि उत्पादक न तो प्रथम चरण में कार्य करेगा और न ही तृतीय चरण में। इसलिए प्रथम और तृतीय चरण को आर्थिक बेतुकापन अथवा आर्थिक निरर्थकता के चरण कहा जाता है। इस प्रकार, चरण I और III उत्पादन फलन में गैर-आर्थिक क्षेत्रों का प्रतिनिधित्व करते हैं।
बढ़ते प्रतिफल के कारण
प्रारंभ में उत्पादन के स्थिर कारक की मात्रा, परिवर्तनीय कारक की मात्रा की तुलना में अधिक होती है। इसलिए जब अधिक परिवर्तनीय कारक जोड़े जाते हैं, तो स्थिर कारक की दक्षता बढ़ जाती है।
दूसरा कारण यह है कि जैसे-जैसे परिवर्तनीय कारक की अधिक इकाइयों को नियोजित किया जाता है, परिवर्तनीय कारक की दक्षता स्वयं बढ़ जाती है। इसका कारण यह है कि जब परिवर्तनीय कारक की पर्याप्त मात्रा होती है, तो श्रम का विभाजन या विशेषज्ञता संभव हो जाती है, जिसके परिणामस्वरूप उत्पादकता अधिक हो जाती है।
घटते प्रतिफल के कारण
जैसे ही एक ऐसा बिंदु आता है जहाँ परिवर्तनीय कारक की मात्रा स्थिर कारकों के कुशल उपयोग को सुनिश्चित करने के लिए पर्याप्त हो जाती है, उसके बाद परिवर्तनीय कारक में किसी भी और वृद्धि से सीमांत तथा औसत उत्पाद घटने लगते हैं, क्योंकि स्थिर कारक परिवर्तनीय कारकों की तुलना में अपर्याप्त हो जाते हैं।
श्रीमती जोन रॉबिन्सन ने आगे कहा कि हमें घटते प्रतिफल इसलिए प्राप्त होते हैं क्योंकि उत्पादन के कारक एक-दूसरे के पूर्ण प्रतिस्थापन नहीं होते। अतः, एक बिंदु के बाद अधिक स्थिर कारकों की आवश्यकता को परिवर्तनीय उत्पादन कारकों को बढ़ाकर प्रतिस्थापित नहीं किया जा सकता।
अतः, घटते प्रतिफल इसलिए कार्य करते हैं क्योंकि कारकों के बीच प्रतिस्थापन की लोच असीमित नहीं होती।